Symmetry Meaning
Table of Contents
The word symmetry comes from a Greek word that means ‘to measure together’ and is widely used in the study of geometry. Mathematically, symmetry means that one shape becomes exactly another when you move it in some way: you twist it, flip it, or slide it.
What is Symmetry in Math?
For two objects to be symmetrical, they must have the same size and shape, with one object having a different orientation from the first. There can also be symmetry in an object, such as the face. If you draw a line of symmetry right in the center of your face, you can check that the left side is a mirror image of the right side. Not all objects are symmetric. If an object is not symmetric it is called asymmetric.
Symmetry Definition
When working with symmetry, the initial image is called a pre-image, and the second image is called an image because it is the last step in the process. The last step in that process is the same as the answer to a math problem, the image is what is created by rotating something 90 degrees or by rotating it on its own axis. There are three basic types of symmetry: rotational symmetry, axial symmetry, and central symmetry.
Look at yourself in the mirror. Is one side of your face exactly the same as the other? There may be slight differences, but your face is symmetrical. We are going to learn more about symmetry.
What is the Axis of Symmetry? Axis of Symmetry Definition
The axis of symmetry or axial symmetry divides the shape into two identical parts. An axis is a line that can be vertical, horizontal, or diagonal. Use the following principle to find out if a shape is symmetric:
“Take a shape and you can see if there is an axis of symmetry when you try to bend it and see that the two halves match”.
If we look at ourselves, we have two hands, feet, eyes, ears that are the same. Our nose can also be divided into two symmetrical parts. But if we do it from the side and fold it, we do not get symmetric shapes since one part is the back of the head and the other is the face.
In the examples below, if we take an airplane, a butterfly, or a building and bend them, we get symmetric shapes.

When a shape is rotated 180 degrees, it is the same and it is also the same when it is flipped. If we play cards, we see that they have axial symmetry since they are similar from top to bottom and even if we cut diagonally.

Examples of Symmetry
Symmetry in Alphabets a-z
The letters A, M and U have axial symmetry while B and K have horizontal symmetry. S and Z have axial symmetry. But the letters F, G, P, and R don’t have symmetry.

Symmetry in Real life: Symmetry in Nature
If you look closely at the bee hives, you will see hexagonal symmetry in each circle allowing maximum storage of honey.
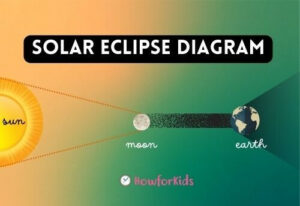
Why does the big sun and the small moon appear to be the same size during a solar eclipse? The sun is 400 times bigger than the moon and is 400 times farther away than the moon, therefore they symmetrically appear the same size.
Read also: Solar System for kids
Types of Symmetry
We can find symmetry everywhere. Symmetry occurs when there is an exact shape of an object around a certain line called the symmetric axis. In a symmetrical pattern, a particular part of the design is repeated over and over again to achieve perfect symmetry.

Geometric symmetry has three types:
- Reflectional symmetry
It can be found in geometric figures, in mathematics, in nature, and in man-made things. In this topic, we will explore the defining characteristics of reflective symmetry as well as some day-to-day examples.
What if you take a photo of yourself, a passport size photo, and draw a line right down the center of your face, from your forehead to your chin? What would you notice? Does one side of your face seem like a reflection of the other? For example, there would be an eye on each side. Both halves of your lips would look almost identical. Unless you had some sort of surgery, the two halves of your nose would look the same.
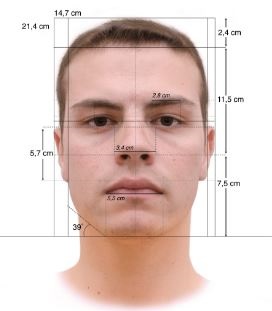
Your ID photo is just one example of reflective symmetry, also known as bilateral, linear, or mirror. The line you draw to divide the face is called the line of symmetry.
However, since humans have differences that are not controlled, our faces may not always be examples of reflective symmetry. For example, some of us may have a mole on one side, others may have a scar. If you look closely in a mirror, you may notice that one of your eyes is slightly smaller than the other. Many aspects of human appearance can distort the notion of true reflective symmetry; therefore, reflective symmetry must satisfy certain conditions.
Reflective symmetry occurs when a line is used to divide an object or shape into halves so that each one reflects the other half. Sometimes objects or shapes have more than one line of symmetry. For example, the letter H. How many lines of symmetry does it have? If you have answered that two, you are correct. There are two ways to draw a line. line so that each half reflects the other half.
- Rotational Symmetry

The recycle icon is a very common symbol and like most effective icons, the image itself is suggestive. The arrows in the image appear to move in a circular fashion, suggesting the circular concept of recycling. Along with this perspective, if you rotate the image 120 degrees, and another 120 degrees, and another 120 degrees, it would look the same.
This attribute is called rotational symmetry. Many shapes have rotational symmetry, such as rectangles, squares, circles, and all regular polygons. Pick an object and rotate it 180 degrees about its center. If at any point the object is exactly the same as before the rotation, then the object has rotational symmetry.
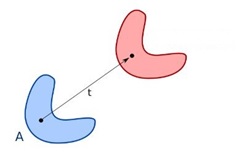
- Translational Symmetry
It is a symmetry in which a particular pattern or design moves from one side to the other. In other words, it is a type of symmetry in which an object changes places without rotating or without reflection. The same image is elsewhere, even the orientation of the image is the same.
Also read: What is an Atom for kids
What is the Center of Mass? Center of an Object.
The center of a shape or an object with rotational symmetry is the point about which the rotation takes place. If a player rotates a basketball on their finger, the tip of the finger would be the center of rotational symmetry. If an object has rotational symmetry, its center will also be its center of balance.